从零开始编写 C 编译器 Chapter 1.2 | Parser

Note: 所有代码、定义、术语命名都参考 Nora Sandler 的书籍 Write a C Compiler

Parser

源代码在经过 Lexer 之后，剔除了无用的部分(如换行、空格等)，形成了一个 token.t 列表。Parser 遍历 token 流，判断某一部分 token 是否能组成正确的语言结构，并把他们抽象为一个结点。将不同的结点分层，最终组成一棵抽象语法树(Abstract Syntax Tree, AST)。

线性的 token 流失去了源码的结构性，很难处理嵌套的子结构及分支结构等。AST 的树形结构天然具有递归性，能很容易的进行递归甚至回溯，是更符合机器体质的数据结构。

一般来说，语法错误都是在 Parse 阶段判断的，在生成 AST 之后，编译器只保留了程序的语义结构，但省略了具体的语法细节(如分号、括号)，因此称为 “抽象”语法树。本质上 Lexer 和 Parser 都是对源代码的抽象，最终保留下来核心的语义信息交给后续部分生成 Assembly Code。

AST 的一个例子

考虑如下的 if-statement 语句。

1
2
3

if (a < b) {
    return 2 + 2;
}

其对应的 AST 中，根节点表示整个 if 语句，并有两个子节点：

左子树: The condition a < b
右子树: The statement return 2 + 2

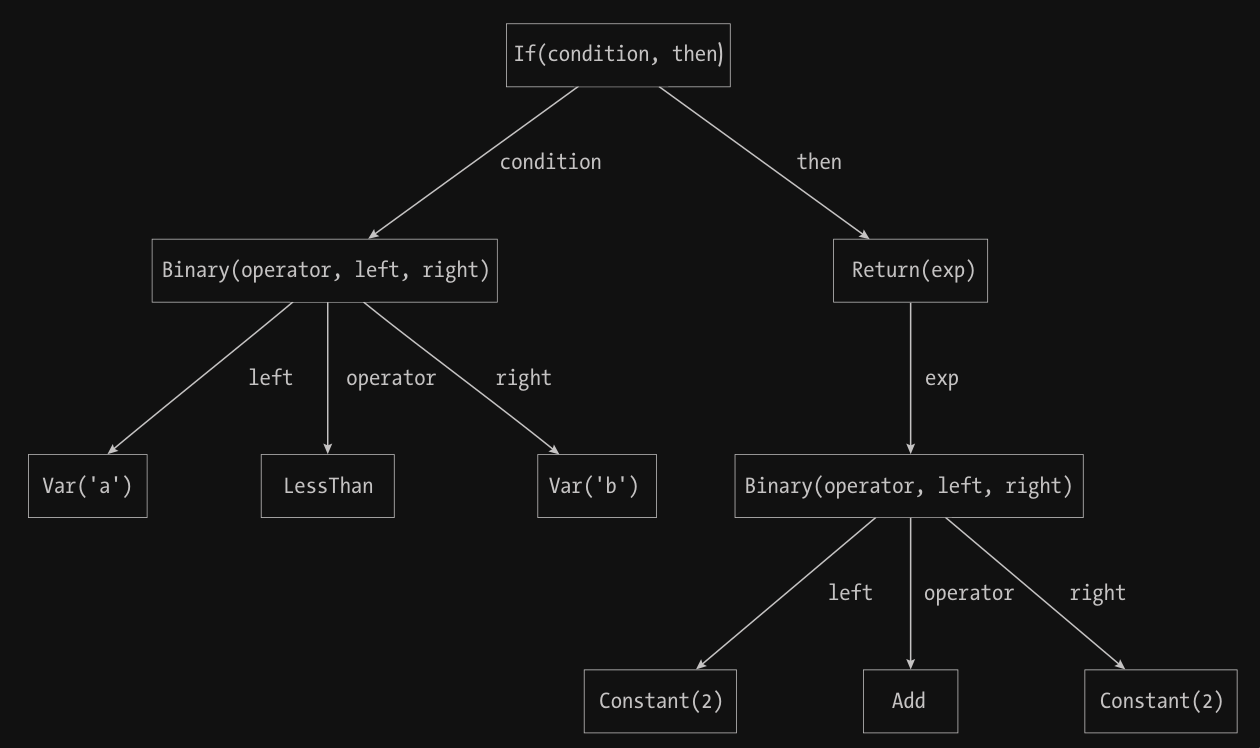
我们还可以对每个子节点定义更细致的孙结点: 表达式、二元运算符、左操作数、右操作数等。上述 if 语句的完整 AST 见下图：

对于本章给出的 C 程序 return_2.c，它的 AST 会更加简单。如下图所示，这是一个线性的树型结构。

AST 所保留的语义信息和源代码是同等的，即我们可以从源代码生成一棵 AST，同样也可以从一棵 AST 还原回源代码。这条性质在后续 debug 的时候很重要。

AST 的定义

我们使用 Zephyr Abstract Syntax Description Language(ASDL) 语言来描述一棵 AST。对于 return_2.c 的AST，我们可以定义为如下：

program = Program(function_definitions)
function_definition = Function(identifier name, statement body)
statement = Return(exp)
exp = Constant(int)

每一行都定义了一个 AST 的结点。根节点是 Program 结点，其子节点(或子节点们)为一个元素类型为 function_definition 的列表的结点。但目前我们只有 main 函数，所以只有一个子节点。一个 function_definition 结点有两个子节点: 用于表示函数名的 identifier 结点和表明语句的 statement 结点。之后还可能新增参数节点(argument node)。目前我们只有 return 语句，所以只有一种 statement 结点，且它的唯一子节点为一个 exp 结点。同样， exp 结点只有一种，它只代表一个 int 类型的常数。

我们可以通过 | 来为一类结点添加新的变体 constructor。例如：

1	`statement = Return(exp) \| If(exp condition, statement then, statement? else)`

此时 statement 的值可以为Return 或 If。若为 If 结点时，有3个子节点，分别为表明判断条件的 exp 结点，条件满足时候的执行的 statement 结点，和不满足时执行的 statement 结点。statement? 中的 ? 表明此子节点是可选的，因为不是所有的 if 语句都有 else。

形式文法 (Formal Grammar)

上述 ASDL 语句只定义了每个结点所包含的信息，我们还需要一套从 token 序列构建 AST 的规则。比如 return 语句结束时必须跟着一个 ;，函数体必须包裹在 {} 中等等。这套规则我们叫作 形式文法(Formal Grammar) 。对于 return_2.c 的 AST，每种结点所对应的形式文法如下：

<program> ::= <function>
<function> ::= "int" <identifier> "(" "void" ")" "{" <statement> "}"
<statement> ::= "return" <exp> ";"
<exp> ::= <int>
<identifier> ::= ? An identifier token ?
<int> ::= ? A constant token ?

本文采用 extended Backus-Naur form (EBNF) 记号，每一行都是一条产生式规则 (productioin rule)，用于定义一个语言结构如何由其他语言结构和 token 组成。用 <> 括起来的符号叫作 非终结符(non-terminal symbols)，而单一的 token 称作 终结符(terminal symbols)。非终结符可以在产生式左侧出现、并可被进一步替换或展开的符号。它们不代表语言中的实际字符或词法单元，而是代表语法结构的抽象类别。由于 identifier 和 int 在源代码中并不是固定的，我们使用两个 ? 将其包裹起来。

在上述定义中，<function> 后的语句规定了，一个合法的函数定义必须包括: 一个 int 类型的 token，后跟着一个 Identifier 类型的 token，再后面是左括号、void、右括号等等。只要有一段 token 序列满足这个定义，就可以将其合成为一个 function 结点。

如果我们想对非终结符 statement 增加一类 if 语句，可以通过如下的产生式规则来定义其语法。[] 表示可选部分。

1 2	`<statement> ::= "return" <exp> ";" \| "if" "(" <exp> ")" <statement> [ "else" <statement> ]`

递归下降解析 (Recursive Descen Parsing)

RDP 是一种自顶向下的语法分析方法，通过为文法中的每个 非终结符 编写一个对应的 token 转换函数来实现对输入 token 流的解析。

更详细的描述为：给定一组形式文法，递归下降解析器为每个非终结符 \(A\) 构造一个解析器 parse_A()。该解析器：

读取当前输入流中的词法单元（token）；
根据文法中 \(A\) 的产生式规则，决定使用哪一条规则进行展开；
递归调用其他非终结符对应的解析器，直至语句解析完毕，或 token 消耗完毕；
若解析成功，则消耗相应 token，并生成对应的 AST 结点；若失败，则可报错或回溯。

例如，对于 return_2.c 的 Parser，解析 statement 语句可为如下伪代码：

parse_statement(tokens):
    expect("return", tokens)
    return_val = parse_exp(tokens)
    expect(";", tokens)
    return Return(return_val)

expect(expected, tokens):
    actual = take_token(tokens)
    if actual != expected:
        fail("Syntax error")

当这个位置期待有一条 statement 时，我们调用 parse_statement 解析器。根据形式文法，statement 需要由三部分组成：return 关键字，一个 exp 符号，以及一个 ;。通过复杂函数 expect 判断下一个 token 是否是 Return，之后递归的调用 parse_exp 来解析 exp 符号。这也是这种解析方法被称为 ”递归下降“ 的原因。由于 program 结点中包括了所有的 function_definition，同时也理应包括了所有的 exp，所以调用 parse_program 就能递归的解析完所有的产生式规则，并生成对应的 AST。

当一个 AST 结点可由多条产生式规则生成时(如 return 和 if 都对应一个 statement 结点)，可以根据首部的几个 token 决定使用哪条路径，或可以采用回溯的方法枚举所有的规则。

Implementation

首先定义 ast 结点。每类结点使用一个枚举体即可：

type exp = Constant of int
type statement = Return of exp
type function_definition = Function of 
  {name : string; body : statement}

type t = Program of function_definition

可以使用 流式输入 来维护 token 流:

let take_token tokens =
  try Stream.next tokens with Stream.Failure -> raise End_of_stream

(* convert a list to a stream *)
let of_list lst = Stream.of_list lst

对于每类结点，根据产生式规则编写一个 parse，消耗 token 并生成对应的 AST 结点

let parse_id tokens = 
  match Tok_stream.take_token tokens with
  | T.Identifier x -> x
  | other -> raise_error ~expected:(Name "an identifier") ~actual:other

let parse_int tokens = 
  match Tok_stream.take_token tokens with
  | T.Constant c -> Ast.Constant c
  | _ -> raise (ParserError "Syntax error")

let parse_exp tokens = 
  parse_int tokens

let parse_statement tokens = 
  let _ = expect T.KWReturn tokens in
  let return_val = parse_exp tokens in
  let _ = expect T.Semicolon tokens in
  Ast.Return return_val

let parse_function_definition tokens = 
  let _ = expect T.KWInt tokens in
  let fun_name = parse_id tokens in
  let _ = expect T.OpenParen tokens in
  let _ = expect T.KWVoid tokens in
  let _ = expect T.CloseParen tokens in
  let _ = expect T.OpenBrace tokens in
  let statement = parse_statement tokens in
  let _ = expect T.CloseBrace tokens in
  Ast.Function {name=fun_name; body=statement}

let parse_program tokens = 
  let fun_def = parse_function_definition tokens in
  if Tok_stream.is_empty tokens then Ast.Program fun_def
  else raise (ParserError "Unexpected tokens after function definition")

最后调用 parse_program，生成合法的 AST，并检查是否还有剩余的 token 。

let parser tokens = 
  try 
    let token_stream = Tok_stream.of_list tokens in
    let ast = Private.parse_program token_stream
  with Tok_stream.End_of_stream
  -> raise (ParserError "Unexpected end of file")

最后的碎碎念

从 AST 的构建过程就可以看出 函数式编程 对处理数据结构的优越性。对于一棵树结构，我们不用维护繁琐的 lchild 和 rchild 指针，也不用显示指明有多少儿子。

在函数式语言中，实现一棵树型结构是通过元组来实现的，例如对于二叉树，我们可以很简单的定义如下类型：

1
2
3

type binary_tree = 
  | Empty
  | Node of int * binary_tree * binary_tree

对于如下的二叉树，它的实际表示为：

Node (1,
      Node (2,
            Node (4, Empty, Empty),
            Node (5, Empty, Empty)),
      Node (3, Empty, Empty)
     )

即一个嵌套 \(3\) 元组 (1, (2, (4, Empty, Empty), (5, Empty, Empty)), (3, Empty, Empty))

对于我们的 AST 也是同理，只需要几种不同的一元组(因为目前 AST 是线性的) 即可。对于 program 结点，包括一个 function_def 结点。function_def 包括一个结构体，其中的 body 字段包括一个 statement 结点，而这个 statement 结点包括一个 exp 结点。本质上这棵 AST 可表示为 program(func_def(name; body(exp(int)))) 我们不需要频繁的维护 next 指针，只需要将递归生成的子节点放在元组对应的阶段即可。想象一下如果用 cpp 编写同样的 AST，需要对不同的结点定义不同类型的 next 指针，可能还需要一系列的抽象基类、继承、多态。

compiler

#compiler

从零开始编写 C 编译器 Chapter 1.2 | Parser

https://acmicpc.top/2026/01/16/write_a_c_compiler/Chapter1.2-Parser/

作者

江欣婷

发布于

2026年1月16日

许可协议

从零开始编写 C 编译器 Chapter 1.3 | Codegen 上一篇

从零开始编写 C 编译器 Chapter 1.1 | Lexer 下一篇